Winkel Tripel Warping Trouble
By Evan Miller
October 20, 2012
All programming blogs need at least one post unofficially titled “Indisputable Proof That I Am Awesome.” These are usually my favorite kind of read, as the protagonist starts out with a head full of hubris, becomes mired in self-doubt, struggles on when others would have quit, and then ultimately triumphs over evil (that is to say, slow or buggy computer code), often at the expense of personal hygiene and/or sanity. One such post I have been re-reading with fondness is “Formula Engine Rewrite” by Damien Katz.
I have previously regaled readers with a couple of tales of my own quest for speed in the face of adversity; see here and here. But these were child’s play compared to a story I call Winkel Tripel Warping Trouble, or How I Found a Bug in the Journal of Surveying Engineering. This story sums up what I think software engineering is and ought to be. That is to say, it sums up why, exactly, I am awesome. If for whatever reason you have a problem with the idea that I am awesome, stop reading now. Otherwise, heat up some popcorn, sit back, and enjoy the story of an engineer who wouldn’t take slow for an answer.
**
The story begins in late 2010, when I had some geographic data and wanted to put it onto a map. Seems simple, right? I was starting my third year of graduate school and dutifully signed up for a free two-day intensive course in Geographic Information Systems at the University of Chicago. After two days of wrestling with ArcGIS, ArcEditor, ArcCatalog, and ArcWhatever on the university computers under the gentle guidance of the Local GIS Expert, and feeling no closer to having my stupid points appear on a map, I decided to write a little program of my own.
I didn’t think this would be too hard; I had previously written a program to take a Shapefile, that is, the document format of ArcGIS, and draw it with pretty colors. (This was for an iPhone app I had written the previous summer, which let you listen to Chicago police dispatchers and see a map of where each dispatch was coming from.) So I wrote a new little program to take a Shapefile of states and a CSV file of points and draw them on my Mac.
Of course, if you just take a list of latitude and longitude coordinates and treat them as if they were X-Y coordinates, the result looks quite unnatural. The United States looks short and fat instead of like a geomorphic shield protecting the liberty of the world. To get a map to look like a map, instead of like a computer file from the 1980s, you need to use a map projection.
I spent some time on Wikipedia learning about map projections and settled on four projections for my program that would make my maps look sleek and professional: Mercator (used by Google Maps and others), Albers Equal Area, Lambert Conformal Conic, and the Winkel Tripel (used by National Geographic). To implement these map projections I used the excellent Proj.4 library.
All was well and good, except at some point I decided that my program should not just convert latitude and longitude into X-Y coordinates; it should tell you the coordinates where you are clicking, that is, convert X-Y coordinates back into latitude and longitude.
Calculating the reverse projection is usually straightforward, and the needed routines were available in the Proj.4 library — except, oddly, for the Winkel Tripel projection. I was not about to abandon the official map projection of National Geographic on account of a deficiency in Proj.4, so I set about to find the reverse projection formulas for Winkel Tripel.
As it turned out, Winkel Tripel is a sort of map projection bastard, the result of an unholy union between ellipsoidal Aitoff projection and a rectangular projection. As a consequence, there is no clean analytic formula for recovering the original latitude and longitude from the projected X-Y coordinates. You have to use messy numerical techniques to guess-and-check until you get “close enough” to the right answer.
All of this was described in great detail in two relatively recent papers I found online, “An Inverse Solution to the Winkel Tripel Projection using Partial Derivatives,” and its companion piece, “A Computer Program For The Inverse Transformation of The Winkel Projection.” The first paper described how to apply Newton’s method to the Winkel Tripel formulas — a neat idea, and in retrospect, completely obvious — and the second paper provided a FORTRAN implementation, which I carefully ported to C for use in my program. I tested it out, and it worked like a charm; you could click anywhere and see the latitude and longitude of the click, even with the infamous Winkel Tripel projection that had dogged GIS programmers for decades (and me for only a week, thanks to these great papers I had found).
**
Fast-forward about six months. I was working feverishly on another project and had hit a wall. For distraction I decided to revisit my maps program and see if I could implement a feature that I thought would make for slick marketing materials: projecting raster images onto my maps, and projecting them quickly enough that you could change the projection parameters in real-time.
After looking at other image warpers, I thought they were too complicated. They projected each point on the image into X-Y space and then interpolated any missing pixels in the resulting image. This seemed backwards to me, since you ended up projecting a lot of points you didn’t need; a better solution in my mind was to take each pixel on the screen, run the reverse projection and find out where it hit the image (if at all), and then interpolate the pixel color value using the surrounding points in the image.
Within a couple days I got some basic code working, but it was slow, and definitely unusable. To speed things up I rewrote the projection routines in OpenCL, which seemed to be about 5 times faster than the Proj.4 library I had been using. I also wrote the image-sampling logic in OpenCL, which made real-time image warping just barely usable — except when it came to the Winkel Tripel projection, which was orders of magnitude slower than all of the others.
I knew that Winkel Tripel would be slower than the others, since it used an iterative method for the reverse projection, whereas Mercator and the rest used nice, clean, one-shot analytic formulae. But it was 10, 20, even 50 times slower than Mercator, and completely unusable. Herein lies the difference, in my mind, between the True Engineer, like me, and the Wannabe Engineer. Rather than abandon the Winkel Tripel projection in favor of a less computationally intensive projection that looks nearly as good, which is the rational and sane thing to do, I decided I would improve on Newton’s method, which, being named after the famous physicist, you might say had withstood the test of time.
Newton’s method works by taking the first derivative of the formula you’re solving; given an incorrect solution, this derivative essentially points you in the direction of the correct solution starting from the incorrect solution. From my Winkel Tripel tests, Newton’s method seemed to be consistently undershooting the correct answer by about 10-30%, and so it took a while to converge (10 iterations in the best case, 90 iterations in the worst case).
Well, I thought, why not use two derivatives to compensate for how the first derivative shifts between the incorrect answer and the correct answer? Winkel Tripel doesn’t seem to show a lot of curvature, so I figured the second derivative would fix any undershooting and nail the correct answer in just a few iterations.
After hunting around on Google and Wikipedia, I discovered that this is two-derivative approach is called Halley’s method, and is about 300 years old — so much for having anything named after me. I found a paper with the formulas for solving simultaneous equations with Halley’s method, and set about finding the second derivatives I would need for the job. I spent three days in coffee shops with a pen and paper taking first and then second derivatives of the Winkel Tripel formula, and double-checking them until I was finally satisfied that I had discovered their most simple forms. As soon as I was done, I rushed home, and in a couple of hours, I coded up the modifications to Newton’s method, crossed my fingers, and ran the modified program.
And… nothing! Halley’s method showed absolutely no improvement over Newton’s method in terms of how many iterations it needed to converge. Worse, since each iteration was more computationally intensive, the program was two times slower overall.
At this point, any sane person would admit defeat and just pick another map projection that is simpler to compute. But something bothered me: it was mathematically impossible for Halley’s method to undershoot the correct answer by the same amount as Newton’s method, and yet that is exactly what I was seeing. I realized something there must be something wrong not in my idea, but in my code.
So I checked all my code. I checked it again. I rederived all my derivatives. I checked to see that I had correctly ported the FORTRAN code for Newton’s method to OpenCL, but I could not for the life of me find the bug. Now I was pissed. At this point I knew my code was correct, but I also knew there had to be a bug somewhere in the 25 short lines of OpenCL code on my screen. I sat and stared, running my eyes over the code, checking this, checking that.
And there it was. I noticed that in the Newton’s method part of the code, the part I ported had from FORTRAN, the part I had assumed was correct, two terms were being added together when they should have been multiplied. That was odd, since I had checked my port of the FORTRAN code several times over. So for yucks I went back to the original paper, and… the bug was there, too! The original code had implemented Newton’s method incorrectly, and their program converged much more slowly than it should have. In addition to causing me several days of pain and suffering, all of the convergence results reported in the paper were wrong.
How bad was the bug? Well, after replacing the plus sign with an asterisk, and ripping out Halley’s method, the method converged in 3-8 iterations instead of the original 10-50 iterations. I then realized that the authors’ initial guess for Newton’s method was not a very good one; by plugging in a better initial guess, I got the algorithm to converge in 2-4 iterations — a 5-20X speedup overall. Since Halley’s method was twice as computationally expensive as Newton’s method and only knocked off an iteration or two from the convergence, it turned out to be slightly slower overall, so I abandoned it. So much for three days of taking derivatives in coffee shops.
But at this point, by fixing this simple bug, Winkel Tripel was finally in the same ballpark as Mercator as far as projecting images was concerned; still slower, but with a few more optimizations, it finally became usable. I could now reproject images in real-time as if they were made of rubber. I soon shipped the feature, and now the first screenshot you see for the Magic Maps on the App Store is this:
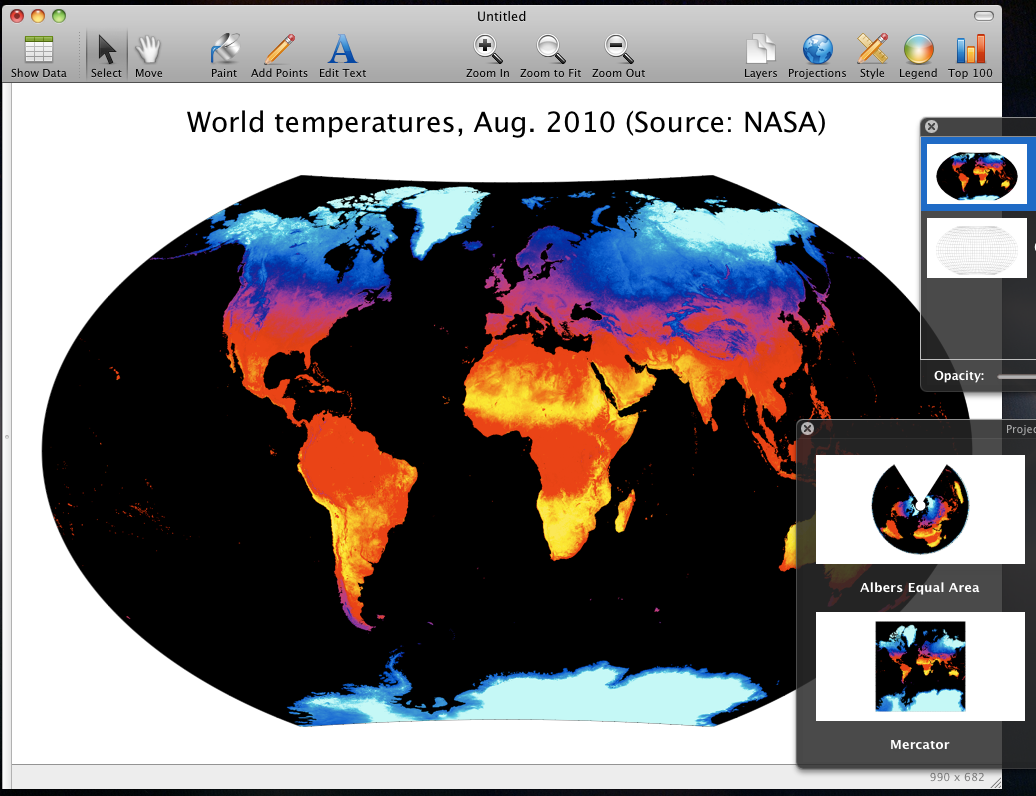
Figure 1: A minor feat of software engineering.
I emailed the authors of the Newton’s method paper, and they graciously acknowledged their mistake and thanked me for my suggestion about a better initial guess. They said they would soon look into the issues I raised and report back; that was about a year ago, but perhaps not surprisingly, I still haven’t heard anything.
You’re reading evanmiller.org, a random collection of math, tech, and musings. If you liked this you might also enjoy:
Get new articles as they’re published, via LinkedIn, Twitter, or RSS.
Want to look for statistical patterns in your MySQL, PostgreSQL, or SQLite database? My desktop statistics software Wizard can help you analyze more data in less time and communicate discoveries visually without spending days struggling with pointless command syntax. Check it out!
Back to Evan Miller’s home page – Subscribe to RSS – LinkedIn – Twitter